Zero-Level-Set Encoder for Neural Distance Fields
Stefan Rhys Jeske, Jonathan Klein, Dominik L. Michels, and Jan Bender
Abstract
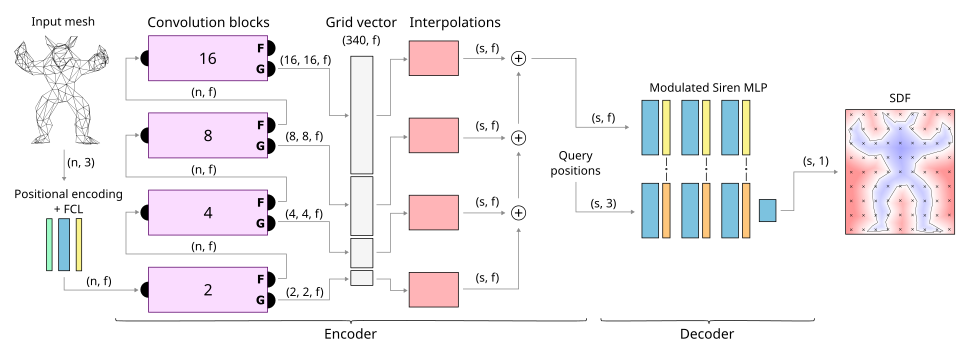
Neural shape representation generally refers to representing 3D geometry using neural networks, e.g., to compute a signed distance or occupancy value at a specific spatial position. Previous methods tend to rely on the auto-decoder paradigm, which often requires densely-sampled and accurate signed distances to be known during training and testing, as well as an additional optimization loop during inference. This introduces a lot of computational overhead, in addition to having to compute signed distances analytically, even during testing. In this paper, we present a novel encoder-decoder neural network for embedding 3D shapes in a single forward pass. Our architecture is based on a multi-scale hybrid system incorporating graph-based and voxel-based components, as well as a continuously differentiable decoder. Furthermore, the network is trained to solve the Eikonal equation and only requires knowledge of the zero-level set for training and inference. Additional volumetric samples can be generated on-the-fly, and incorporated in an unsupervised manner. This means that in contrast to most previous work, our network is able to output valid signed distance fields without explicit prior knowledge of non-zero distance values or shape occupancy. In other words, our network computes approximate solutions to the boundary-valued Eikonal equation. It also requires only a single forward pass during inference, instead of the common latent code optimization. We further propose a modification of the loss function in case that surface normals are not well defined, e.g., in the context of non-watertight surface-meshes and non-manifold geometry. We finally demonstrate the efficacy, generalizability and scalability of our method on datasets consisting of deforming 3D shapes, single class encoding and multiclass encoding, showcasing a wide range of possible applications.
Paper
In: arXiv, 2024
Link: https://arxiv.org/abs/2310.06644
Download:

Citation
@Article{Jeske2023_ndf_encoder,
author = {Jeske, Stefan Rhys and Klein, Jonathan and Michels, Dominik L. and Bender, Jan},
title = {Zero-Level-Set Encoder for Neural Distance Fields},
journal = {arXiv},
year = {2024},
month = {8}
doi = {10.48550/arXiv.2310.06644},
}

